Prenons un repère orthonormé et étudions les possibilités pour relier le point A (1,0) au point B (0,1) en n’effectuant que des déplacements horizontaux ou verticaux.
Le premier qui vient à l’esprit est de partir de A, de monter de 1 et d’aller à gauche de 1 pour rejoindre B, la distance parcourue sera donc égale à 2.
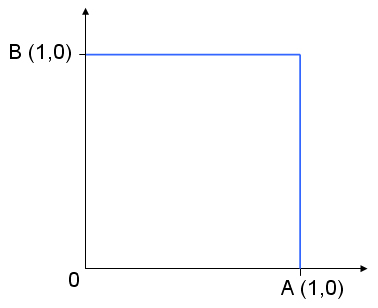
On peut également partir de A, monter de 1/2, aller à gauche de 1/2, remonter de 1/2 et aller de nouveau à gauche de 1/2 pour rejoindre B. On aura toujours parcouru une distance égale à 2.
On peut faire encore la même chose avec 1/4, ... pour obtenir ce que l’on observe sur l’image.

La distance parcourue est toujours égale à 2.
Mais seulement, voilà le problème. Si on effectue l’opération décrite précédemment avec des distances pour les montées et les revirements à gauche qui tendent vers 0, on devrait toujours avoir une distance de 2 et on obtient petit à petit une droite.
Or, la distance de cette droite n’est pas égale à 2 mais à racine carrée de 2 (soit environ 1,4) en tant que diagonale d’un carré de côté 1.
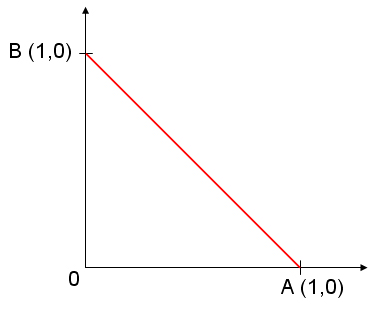
Ce paradoxe est expliqué par Cantor à la fin du XIXe siècle : cela vient d’une différence d’infinis. Les tournants successifs de plus en plus petits "tendent vers l’infini des nombres entiers alors que la droite est l’infini des nombres réels [1]". Le second est beaucoup plus grand que le premier. Les tournants successifs se rapprochent de la droite mais ne peuvent jamais s’identifier à elle.
Le premier infini a été baptisé aleph0 et le second aleph1.

Aucun commentaire:
Enregistrer un commentaire